Rumour has it that there will be New Crystal Maze.
Below is a reading of Sata's official position on the possibility of a revival of the best gameshow ever of all time ever.
https://www.youtube.com/watch?v=jFp_GHDLKaA
Tom's thoughts and ramblings. TV, Games, TV games, and other things. Often Geeky. Often Long.
Tuesday 30 August 2016
Tuesday 23 August 2016
In which the Author remains convinced that ITV know nothing about primetime quizzes
As Dan Peake remarked ITV haven't made a successful primetime quiz since...
[insert your own punchline here].
ITV have, in fact, shown two good quizzes in this author's memory: Duel (2008) and The Exit List (2012). That neither was successful we wholly blame on ITV's decision not to renew.
 |
| Let's Duel. |
In fact, if we discount instances of friendly fire, we think ITV has only made one good quiz at all in recent memory; that being Jenny Ryan's programme. Tipping Point, by the way, does not count because it is an arcade game (not a quiz), and 1000 Heartbeats does not count because it is a multidisciplinary challenge (and/or: we forgot it). That said, we hear Rebound is being afforded a second series - if so then we might afford it a review.
 |
| This is not a picture of Revolution. |
A lot of the demand to create new primetime gameshow things has been absorbed by The Cube, which is a great show, but not a quiz, and is getting a bit old. Perhaps 500Q was ITV's one attempt to find a quiz replacement before reverting to the safer territory of physical games - perhaps it was their attempt to copy the success of The
 |
| #givethatmanapodium |
We're not actually going to pour very much over 500Q itself, mainly because there's not that much which is both interesting and not obvious to the naked eye. The Challengers are a bit redundant. The questions are (slightly) too hard, and there aren't 500 of them. The catchphrase (can you remember what it is? Exactly.) doesn't work. The set's too big. The lack of a destination has been patched, but at the cost of making the game overtly asymmetric. Position in the queue is everything.
 |
| Three wrong and you're... eliminated? |
The problem is, turning our eyes upward, Sata's author knew that 500Q would be a disaster. We've already seen it fail in America - few people watched it and even fewer thought it any good. We've heard that it failed to shine in Germany, and even on paper, it seems obvious to us that 500Q is a weak format: it's just questions, not five hundred of them, not particularly fast, and with no real destination.
 |
| Some of the not 500 Questions. |
What bamboozles us is that heavy resources have gone into producing 500 Questions. They've got (borrowed) an expensive set, the questions are of an ok quality, the editing is tight, and we (subjectively) like Giles. It's not going to set the world alight, but, it is watchable; Sata comfortably sat for an hour. The programme produced could (with some numbers changed) fit comfortably into the 5pm daily position.
And ITV are actually great at this. We haven't bothered writing about many of them, but over the last 2 years we've seen ITV create 4 or 5 middling-to-competent teatime alternatives. (And Freeze Out.) This one just happens to have escaped into a slightly bigger studio, and a slightly later transmission. But we can't just wrap things up there: 500 Questions as a format demands to be primetime, demands to be eventful, demands to be Big. For it to be a mediocre hour, is, due to its own nature, a failure.
We think everything wrong with the Format 500 Questions is endemic; no amount of work could save it. We cite the programme produced by ITV as evidence. What we find most annoying is that this wasn't an easy mistake to make. We think any ITV exec could and should have noticed that 500Q was a lacking format, and we think the same work done on a blank slate would probably produce something adequate; maybe even another Exit List or Duel, (which the channel could then inappropriately cancel, obviously).
We ranted last summer that BBC4 had had one successful gameshow and then given up trying. We might contrast ITV, who have almost given up on primetime quizzes, and who we doubt have the insight to ever get one right.
Monday 25 July 2016
Pyrrhic Defeats and Pyrrhic Victories
Sata's pet theory that the demise of Top Gear might be the
best thing that's ever happened for television continues to be proven correct.
This week Robot Wars returned to fill in the Sunday night slot, and we also
know a second series of it-grew-on-us-ok Sata favourite Ultimate Hell Fortnight is in the pipeline.
And now this! The Weaver, an author doing the same thing as
us, only better and more frequently, brought our attention to the revival
(inappropriately advertised as a "new series") of Time Commanders.
The reader will, of course, remember Time Commanders from its much-loved
original 2 series in 2003 and 2005. If not, most of the shows are available to
seek out online.
The premise was pretty simple, Glen Hugill Eddie Mair
(or later, an annoyingly childish incarnation of Richard Hammond) would
grumpily insist that a team of four players played a game of Rome: Total War
(which had been modified 'a bit' but in no noticeable way), against an unseen
team who were never mentioned. The challenge was either to maintain or
overwrite history, and bring glory to the players' nominated side.
Oh, well, nearly. We say a team of four played Rome : Total
War, in fact the team of four had two players each controlling one half of the nominated
army (in the game sense there were two allied and visually identical players
being controlled by the team).
Oh, except having in players who knew RTW would be boring,
and teaching the team RTW's controls on the day would probably lead to a lot of
(equally boring) "what does this button do / how do I
charge/fight/run?" moments, for a UI is a subtle thing, so the team of
four controlled two technicians who controlled two virtual sides who together
constituted the teams forces.
Oh, except how do four people give orders to two people?
Well, two of the team are nominated 'Lieutenants' (later captains), and each
work with one technician. They have more information, more control, and more
focus on what's going on. The remaining
two were 'Generals', which is a higher rank than lieutenant, and were in theory
responsible for the 'broad strokes' of the battle, grand strategies and key
choices.
If this system seems like a bad way to play RTW to you, then
you're missing the point. Whilst one twitchy RTS veteran hunched intensely over
a computer would probably give the Romans (for it is always them) a better
chance of overcoming the Goths (or whoever) at this week's fixture, it would
also give a spectacularly boring programme.
Imagine, if you will, four people all trying to drive a dual-control car. By having the team's tasks distributed; having the grand
planners and the watchers separated from the directors, and having each half of
the force controlled separately anyway, the process of play becomes vocal and
complicated. Not only does each team member need to communicate their thoughts,
but they often need to justify them and add detail.
 |
| Backseat Drivers. |
Communication was a big part of the challenge of Time
Commanders, and one completely orthogonal to the dry strategy the computergame
provided. But communication (in contrast to the computergame) is something very
easy for the audience to follow. In the Battle of Cynocephalae, the first story
is the story of one man trying to do everything and shouting quite frequently,
while the three women around him slowly (and rather independently) learn how to
operate. This story requires almost no telling, and we're reminded of our
comments from the Hunted review about using television as primary and secondary
evidence of the things that have happened.
But, and perhaps by accident, in their mission to make a
computer game into dynamic and compelling television, the designers of Time
Commanders also made a game that was conceptually
extremely appropriate. What do we mean by this? Well, controlling an army is
extremely difficult.
When a player sits down to play an RTS, they have a near
perfect-control setup. They can see everything their own forces can see
(sometimes more) reliably, instantly, and in detail. They can issue orders and
have those orders immediately implemented. They have a lexicon of statistics,
they can know the exact numbers left in the battle, the exact power and health
of each unit at all times.
Time Commanders removed all of these control advantages: a
view of anything more than a small area had to be recreated using blocks on the
map by the generals (later, could be requested using a third technician),
orders had to pass from general to lieutenant to technician to machine, and
information about the mathematical nature of the computer game was kept deeply
hidden, with all clues and prompting to the players presented through the lens
of the historical story.
 |
| The series 2 set had a lot more red. |
And my goodness,
how excellently all these debuffs made Time Commanders capture the feeling of
the chaos of battlefield tactics. Hence, Time Commanders was itself a great
computer game, (despite never letting its players touch a computer) much
greater than RTW and perhaps the best historical RTS ever created.
And it was played only 24 times. Crazy, huh?
(A fair disclaimer: this author has never actually been
involved in a ancient or medieval battle, and is mainly basing opinion on their
memory of films like 300).
In order that the audience could make sense of what was
going on, our experience frequently cut away to commentary from a pair of
experts, one of whom was always the phenomenal Dr Nusbacher. To return to our example of Cynocephalae, the second story of that episode is the story of an Army being mislead in the early stages, but through a series of lucky key moments coming to dominate a battle - this story is only made available to the audience by the experts telling, it's secondary evidence. Pleasingly, though, it's secondary evidence which has been so excellently evidenced with clips from the team and the simulation that we don't ever feel spoon-fed.
The experts made
an incredible contribution to the show, from intimidating the team during the
opening with their slightly shouty explanation of the scenario right through to
the all-becoming-clear postmortem carried out with blocks on the battlemap. They had more work to do when the teams (and plenty
did) gelled smoothly and communicated well, but chose the wrong tactic; sending
cavalry in against spearmen or whatever, because this wouldn't have been particularly
compelling television, but for some reason (perhaps the American's passionate wailing as,
indeed, horses are impaled on spears) on Time Commanders it was.
 |
| "You've been rubbish and you got everyone killed" |
The main playing of the game took up about 50% of the
programme, which the other half containing chatter, history, and a sort of
warm-up "Skirmish", as well as the always-gleeful expert debrief.
Over the different series the exact content here was refined, although we think
the skirmish felt a little bit long for what it was.
There were, we hardly feel we need to mention, no prizes on Time Commanders. There was no banker-style character for everyone to root against. The experts were presented as stern critics, but completely fair, completely lovely, and completely game for the show's surreality. And everyone got on. Relationships were never frayed, social dynamics were never challenged, and everything was done with a smile.
Time Commanders is a show we remember extremely fondly, but
perhaps with a little of the rose-tinting of nostalgia. We actually thought it was Nintendo Hard, but on checking the win rate was only just below 50%. While revisiting the
programme for this review, we noticed little niggles which we hadn't spotted
before; heavy editing to emphasise a clear (enough),
making-the-history-relevant narrative was felt in a few places, the
lieutenants' stories are emphasised much less than the generals', and the first
half of the show lacked the energy of the second half.
We're intrigued by the potential of a 2016 version of TC.
Apparently episodes will now feature 2 teams of 3 people, competing
head-to-screen-to-head. We like the idea of TC as a competition, we think it
could inject more energy into the pre-battle scenes, and put more pressure on
the participants. We are unsure about the teams reducing to three - we imagine
this will mean only one general: more cohesion, less discussion.
We noticed on review how much the aesthetics and sound of
original Time Commanders was influenced by Gladiator - we tried to think of a 2010s equivalent of the massively iconic and popular 2000 film, and our best guess
was HBO's Game of Thrones. Fort Boyard has already gone that way.
We're also interested to see what 10 years of computer
progress will do to the battle simulations; whether more time periods and parts
of the world will be represented, whether elements like artillery and ships
could be included in the game. We're also excited to see if the experts will
return, what sort of shape their role will take in a competition format.
The overwhelming emotion we drew from revisiting Time
Commanders was joy. The teams are always excited and enthusiastic, the experts are
excited for the game and pleased to be able to teach us about history on the
side, the host is (over)excited by the energy of the situation. Time Commanders
was a great, fun programme that dared to be clever, and we can't wait for it to
return.
Monday 2 May 2016
The Maths of The Code -- Part 2/2
We continue from part 1...
 |
| We doubt the laptop is turned on. |
The question I wanted to answer - the question that first
occurred to me after watching the show, is are
you in a better position after getting one question if you pick a number or
miss? Hitting a number is presented
by Allwright as an always-good option, but in the first round, hitting a
number immediately promotes you to a harder level. On the flipside, it
decreases your likely game length, but not by much. There are intuitive reasons
why it might be good or not good for your game to hit a number straight away,
and no (apparent) way to compare the forces against each other.
I think this
question is a great advert for "using maths", because it's
immediately very not obvious what the answer is. It's even less obvious
that it would change depending on the situation, but that turns out to be the
case. Moreover, once we have the answer, we can (broadly speaking) make sense of it.
Anyway, onto the action. A game of The Code lasts
between 3 and 10 sets. The average game is 8.25 sets, but more than half of
games last 9 or 10 sets. 30% of games go to the last number - this makes sense
because one number has to be the last picked, and 3/10 of the numbers need to
be picked.
Oh, a quick note about combinations. There are 8*9*10
combinations for the code (no repeated digits) - but no-one cares about the
order, so we divide by the 6 orders for each combination to get 120 essentially
different combinations.
I'm going to talk a bit about paths, the routes though the 3 rounds that a game might take. I'll
denote a path by 3 numbers, representing the time spent on each level.
For example, the path (1,1,1) means acing the game -
picking the right numbers on your first 3 guesses. A more 'typical' path might
be something like (2,4,3), answering 2 questions on the first level, 4 on the
second, and 3 on the last.
(Perhaps surprisingly), there are 120 paths through the
game, all equally likely. To best see this, you think about your favourite
order of the 10 digits. (Say, 1234567890). Then each of the 120 equally likely
possible code combinations gives a different path through the game. (Convince
yourself of this if it seems unobvious).
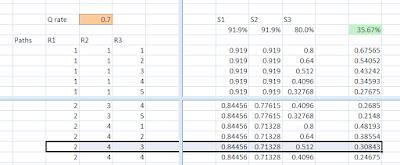
Quite quickly, then, we can find the contestants' chances
of winning the game if they are fated to a certain path - we use the chances of
them surviving each set from part 1, and for the path (a,b,c) and question rate
p, the chance of a win is given:
To give an example, if you know 70% of all questions,
then your chances of winning the game if you were to immediately find 3 numbers:
is 67.5%. If you were destined to the path (2,4,3) which we
mentioned earlier...
your chance of a win is 30.8%.
Next to find the overall probability of winning at the
start of the game. To do this we blur our condition on the path the contestants are
fated to, and since each path is equally likely, it's just like taking an average.
Of course, remembering from last time that R1=R2.
Unfortunately, the distribution of the possible paths
isn't symmetric like it would be if the 3 rounds were independent: a long round
1 likely means a short round 2 and 3. This means we can't really cancel the above into anything more comprehensible. In particular, we can't break down
this formula to get the odds of surviving each round, which will be a shame
later.
We can still put numbers into it, though, and let's set
up a few examples. Suppose Clever Campbell, Borderline Brogan, and Hopeless
Hayden all line up to play the Code. Campbell knows the answer to 90% of
Lesley-Anne's questions, Brogan 70%, and Hayden just 40%.
At the start of the game, we give Campbell a strong 79%
chance to open the safe, Brogan a fighting 36%, and Hayden a mere 5%.
All very good. We're now ready to address the question
that inspired this article - what happens after 1 question?
What's now nice is that because of the uniformity of all
the paths, if we just want to look at some of the paths, say - the paths of
form (1,x,y) that start with getting a number correct - we can just take an average over
those paths that meet the condition. That gives us the odds of success for a
contestant who is destined to get a number on their first guess. [We divide out
by the odds of surviving a round 1 set because we want to model the scenario
that the contestant has got to the point of finding that first number.]
We do this and get the following distribution, for the
chance of winning when you have got one number on the first guess.
Notice Brogan and Hayden have a better chance now -
they've survived one round and are closer to the end of the game. What's
remarkable is that Campbell's winning chance has now gone down, not (just) relative to if they'd guessed a wrong number, but
relative to their position at the start. We'll explore the reason for this
a little later.
For now, let's compare to if the contestants survive one set, but then guess their first number wrong. In this case we just calculate the opposite - the average win probability along all the other paths, and again divide out for the fact the contestants survived one round. Doing so, we find...
For now, let's compare to if the contestants survive one set, but then guess their first number wrong. In this case we just calculate the opposite - the average win probability along all the other paths, and again divide out for the fact the contestants survived one round. Doing so, we find...
every player is in a better position than they were at
the start - this makes sense, they're all facing the same game only with one of
the incorrect numbers removed. What's interesting is that comparing the guessed
correctly and guessed incorrectly scenarios, strong players like Campbell are better off having misguessed, whereas
weak players like Hayden aren't. In the middle players like Brogan are
mostly indifferent to the result of their first guess.
To try to make sense of this, it sometimes helps to
consider the most extreme cases.
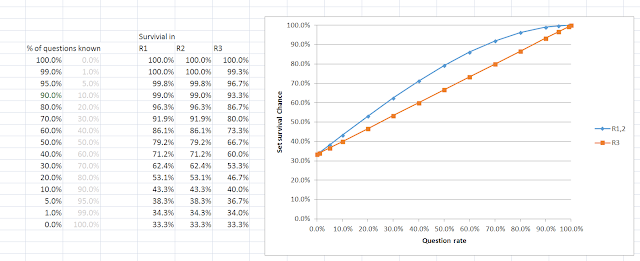
Recall this table from last time, the one telling us
about the relative chances in a R1/R2 and a R3 for different player rates.
Notice for a super bad player, the chances all approach 33% - they're almost
totally reliant on luck - and so R1 and R3 don't look so different. It makes
sense that for them, the better chance comes when the game is likely shorter.
For a super good player the R1 and R3 numbers don't look
too different either - but with numbers this close to 100% we need to be
looking at the chance of failure. For a 99% player, the chance of failing on R3
is around 66 times that of failing in R1, even for Campbell, the ratio is about
6.9 times as much. This makes R3 wildly more important for a good player.
(The reason for this last - to fail on R1/R2, the player
needs to miss at least 2 questions - know any 2/3 and you're certain to answer
correctly. But in R3 the player, 2/3 times can fail having missed only one
question. When the chance of missing a question is small, then the chance of
missing 1 is much larger the chance of missing 2 in a set of 3.)
Accepting that finding the first number first does give a
nudge toward shorter games, and missing it a nudge toward a shorter round 3,
and thinking about the extreme cases, it's hopefully possible to accept this surprising result is intuitive.
Here's a demonstration of something else that might be intuitive: guessing the first number correctly increases the likely length of R3,
and decreases the likely length of the game...
This was intuitive from some angles, but it's worth checking. We want to be sure the 'later rounds get longer' effect from getting the first guess correct doesn't outweigh the 'you're closer to the end now' effect.
In mathematical terms, we (sadly) haven't done any coupling here, we've just arranged the distributa side by side. What's apparent is the intuitive idea that compared to a miss, a hit gives you a longer likely R3, and a shorter likely game.
In mathematical terms, we (sadly) haven't done any coupling here, we've just arranged the distributa side by side. What's apparent is the intuitive idea that compared to a miss, a hit gives you a longer likely R3, and a shorter likely game.
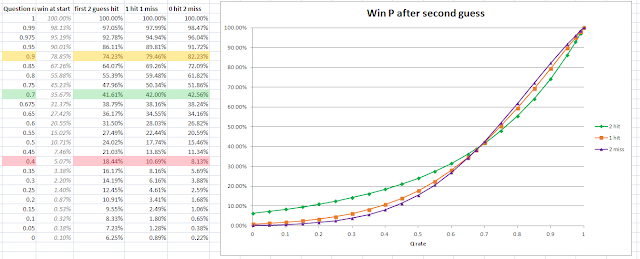
Hopefully, the reader is now in agreement that clever
contestants want to miss on guess number 1, and less clever contestants don't.
But where is the border? Unfortunately, there's not a much better answer to
this than 'where we calculate it to be' - which turns out to be at a question rate of about 67.9%.
One very crude
way we can try to estimate the border is looking at averages. When you hit a
number on the first guess, your R2 and R3 have an average length of 3.33 sets (and
R1 obviously 1), when you miss the average is 3.5 sets for R1, and 2.5 for each
of R2 and R3. So (number of quotes is for effect here) """"on
average"""", getting a hit on guess 1 reduces your (R1+R2)
by 1.67 sets, and increases R3 by 0.83 sets.
If we plot
as a function of the rate, we should see values above one
(denoting an increase in chance of winning) for low question rates and vice
versa for high rates, with the curve hitting 1 around our borderline.
It should be noted before I remark that this estimate
isn't very accurate, that this estimating technique is extremely roundabout. We're ignoring the fact that the round
lengths are not independent variables: when one is low the others are more
likely to be high. We're also ignoring the fact that the these distributions
are being modified in a more complicated way than just a simple "plus
0.8333".
The plot goes like:
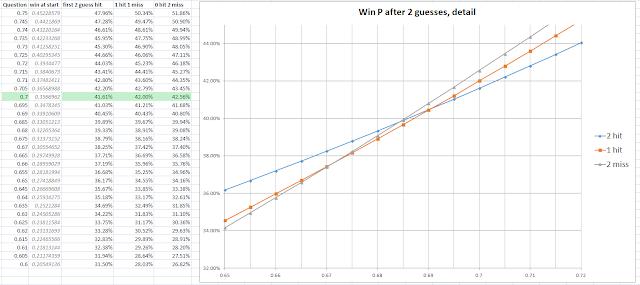
This estimate puts the borderline just above 58% - a fair
way out, but correct in the sense of "it's in the middle". At this
point I have no more elegant arguments to make - the exact value of (about)
67.9% can be found in the ways outlined earlier. That being said, I have a few
more cool facts about the code (but which I'm not going to explain) that I've
found using similar calculations.
Impressively, clever
players are better off if they miss on their first 2 guesses. Less good
players are (unsurprisingly) better off if they get 2/2 on their first 2
guesses. It looked at first like the cut-off point might have been the same
67.9%, but a closer analysis showed:
it was around 68.5%. Also, curiously, there is a very
small margin of skill in which getting 1 hit from the first 2 guesses is worse for
the player than either getting 0 or 2 hits.
What about after 3 guesses? Well, unsurprisingly, the
best result for all players is to get all 3 hits in their first 3 guesses. After
that, though? Here's another graph.
It's worth noting that having 1 digit after 3 guesses and
having 0 digits are nearly indistinguishable. Having 2 digits, though, makes
quite a difference and in accordance with the pattern already established, it's
bad news for clever players and good news for the less clever.
For completeness we include the detail graph for the 3
guesses situation. This time the cutoff is around 67.5%: different again, but not particularly different.
Some closing thoughts then: from observing episodes, we think most contestants on The Code will
generally fall into the "below ~68%" bracket: Matt is right to be
jubilant when the contestants find a number. That said, I think some of the
best contestants will fall into the
"above ~68%" bracket. If you appear
on a future edition of The Code, you are justified in viewing Matt's excitement
when your fist digit goes green as an insult to your knowledge.
We noted at the beginning of part 1 that we assumed the
question difficulty was constant. Since writing that, it has been stated to not be
the case. We think that if the question difficulty increases with the round, the
"good to miss" effect will be even more noticeable than we have
calculated, conversely if the question difficulty increases with the number of
sets faced this effect should be less true than we calculated.
Sunday 1 May 2016
The Maths of The Code - Part 1/2
Hello. We've been watching The Code (not this), the interesting new
BBC quiz, with he-was-quite-good-on-the-exit-list, Matt "are you" Allwright,
and she-wants-to-be-Richard-Osman-well-I-mean-who-on-earth-wouldn't Lesley-Anne
"will probably read this" Brewis.
Our thoughts on the show: It's pretty good. But today on Sata we're not going to talk about The Code as Television, but as The Code maths.
(And I promise that's the last time I do that joke.)
A warning: some of the following will be a bit mathsy, and maybe not accessible to those without a bit of intuition for these things. However, I've tried to keep the amount of 'technical' language to a minimum, (readers who have actually studied maths may even find this annoying) and generally present as much of this as possible in a easy-to-follow way for a non-mathsy audience.
My reasons for doing this are twofold: it makes a (hopefully) more interesting read, and it means you are more likely to believe what I am saying (and this is good because what I am saying is true).
(And I promise that's the last time I do that joke.)
A warning: some of the following will be a bit mathsy, and maybe not accessible to those without a bit of intuition for these things. However, I've tried to keep the amount of 'technical' language to a minimum, (readers who have actually studied maths may even find this annoying) and generally present as much of this as possible in a easy-to-follow way for a non-mathsy audience.
My reasons for doing this are twofold: it makes a (hopefully) more interesting read, and it means you are more likely to believe what I am saying (and this is good because what I am saying is true).
There are going to be two parts to this analysis. In the
first I'll focus on the small scale; the sets of 3 questions that appear on the
Code. My main aim is to produce a formula for the chance of surviving a set, (which we'll need for part 2) and along the way I'll show (surprisingly) that Round 2 is no harder than Round 1. Then in the second, I'll talk about the game as a whole, the lengths of
the rounds, and a team's overall chance of victory.
I'm not going to recite the code's rules; one can watch an episode
or check the comments here. I'll
refer to the sets of 3 questions and 3 answers as "sets", and the
time between before getting each number of the code as the 1st, 2nd and 3rd "round".
For the sake of reasonable maths, I have made the following
assumptions, some of which may be dubious.
1. Aside
from the fact that "you don't see all the questions", the sets don't get more difficult from round to round. (NB: this is confirmed
untrue)
2. Identifying
a correct q/a pair is equally difficult to ruling out an incorrect pair.
3. For
each question, "you either know it or you don't". There are no
hunches, if you don't know 2 questions (or 3), you have a 1/2 (or 1/3) chance
of picking the right one - there is no advantage to comparing two uncertain
questions.
4. On
round 3, there is no advantage to "picking the order" - that is, the
contestants are no more likely to find a question which they know first in the
running than last.
Under these assumptions, I would like to present the claim
that Round 2 is no harder than Round 1 (and round 3 only slightly harder). We start with a wordsy argument to that effect:
If you know the correct question/answer pair, (regardless of
what else you know) you will certainly clear a set in R1. In R2 you'll either
see the correct pair immediately, or discard a wrong pair and then see it. So
in this case R2=R1.
If you don't know the correct pair, but do know that both of
the other pairs are wrong, then by elimination you're also certain to clear a
set in R1, and again in R2 - you'll discard a wrong pair, then be left with a
wrong pair and a mystery pair (which you deduce to be correct).
Suppose you know one of the wrong pairs, but nothing else.
In R1 you have a 1/2 chance of guessing correctly, in R2 you might eliminate
this wrong pair (if you see it), leaving a 1/2 guess, or you might have a 1/2
guess which pair to eliminate (if you don't see it), but then a safe choice
between the remaining two options if you're correct.
Finally, suppose you know nothing about any of the pairs.
Then you have a 1/3 chance of guessing correctly in either round. Hence, in all
cases R1=R2.
Next, we'll briefly consider the best tactics for Round 3.
When faced with the first pair in round 3, if the players have no idea whether
it is right or wrong, we say they should reject it and move along. The best
argument for this is to say that if the contestants take the answer they have a
1/3 chance of being correct, whereas if they reject it they have 2/3 chance of surviving,
then a better-than-1/2 chance of either knowing or guessing the remaining pairs,
making a better than 1/3 chance overall. If they find they don't know on the
second pair, it then doesn't matter - they have a 1/2 chance whatever.
To justify these two arguments more carefully, consider the following work
through of all 24 combinations of question order and knowledge. This will also give us the formula for the chances of getting a
set correct in each round which we'll need later on.
Since we might as well (and it lines up with optimal tactics
for R3), we'll number the questions in each set 1,2,3 based on the order they
are opened, and assume that if contestants are reduced to guessing, they'll
always reject the earliest question and accept the latest question that they
don't know about.
We use a x to represent a wrong pair, and a tick (ok, squareroot
symbol) to represent the right pair. We use brackets (eg: (x)) to mean the
contestants know what the pair is, and the lack of brakets to mean "no
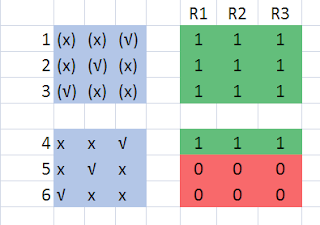
idea". These six cases are obvious, if the contestants know everything,
they always clear the set, and if the know nothing they need to hope they guess
correctly.
Cases 7 through 12 cover all the cases where the contestant
has partial information, but will still guess correctly. In these cases all 3
rounds look the same, because luck favours the contestant.
In cases 15 and 18, being unable to open the last question
means the R3 contestant fails, whereas the R1 and R2 contestants deduce (or
guess, in the case of 15) the correct answer. This is the first time R3 looks
harder than R1 or R2.
Notice in case 15 that the R2 contestant only survives to see by
luck - guessing to reject Q1 rather than Q2. However, the R1 contestant only
picks Q2 over Q1 by luck anyway.
In cases 20, 21 and 23 the R3 contestant's tactics cause
them to reject the correct pair from the start. However, in 20 and 21 the R1 and
R2 contestants guess wrongly anyway - R3 does however see a disadvantage when
they would have known both the following pairs were wrong (19).
Notice in all the cases, R1=R2. It
seems R3 is a bit more difficult than the others, though, there are 3/24 more cases
where R3 loses, although the 24 cases aren't all equally likely.
Now we have to break out more proper maths to asses the likelyhood of each of these 24 cases. In the diagram below I've written the probability of
each state, based on a contestant knowing a proportion p, of all the questions
in the show's repository. We use this to calculate a total probability for
surviving a single set, as a function of p.
We also include the odds of survival if the contestant
guesses randomly rather than for the last question. One can check this gives
the same total in each case. (*The R3 'reject first one if unknown' tactic is
still necessarily used, leading to some of the strangeness in this column.)
We use our table above to calculate a total probability for
surviving a set, as a function of p.
Ok, so, what does this mean in terms of real numbers? Here's your chances of clearing a set in a certain round as a function
of your question rate, p.
"Oh, that's surprising!" says the mathematician in
the audience. "The R3 one looks suspiciously like a straight line to
me." Indeed it does, and upon some algebra, we can confirm:
Is there a good explanation for this? Yes, and in fact we have
one. Suppose the R3 player commits to take the last question if they don't spot
one they know is correct among the first 2. With probability 1/3 the correct
pair lurk at the end, and regardless the player is going to pick it. Otherwise,
with probability 2/3, the contestant needs to notice the correct question when it appears -
they do so with probability p.
Next time, we'll look at the overall game, including the argument that guessing the correct numbers is not always good for you.
Next time, we'll look at the overall game, including the argument that guessing the correct numbers is not always good for you.
----Part 2 ----
Subscribe to:
Posts (Atom)